ਇਸ ਪ੍ਰਕਾਸ਼ਨ ਵਿੱਚ, ਅਸੀਂ ਵਿਚਾਰ ਕਰਾਂਗੇ ਕਿ ਗੌਸੀ ਵਿਧੀ ਕੀ ਹੈ, ਇਸਦੀ ਲੋੜ ਕਿਉਂ ਹੈ, ਅਤੇ ਇਸਦਾ ਸਿਧਾਂਤ ਕੀ ਹੈ। ਅਸੀਂ ਇੱਕ ਵਿਹਾਰਕ ਉਦਾਹਰਨ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਇਹ ਵੀ ਦਿਖਾਵਾਂਗੇ ਕਿ ਰੇਖਿਕ ਸਮੀਕਰਨਾਂ ਦੀ ਇੱਕ ਪ੍ਰਣਾਲੀ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਵਿਧੀ ਨੂੰ ਕਿਵੇਂ ਲਾਗੂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।
ਗੌਸ ਵਿਧੀ ਦਾ ਵਰਣਨ
ਗੌਸ ਵਿਧੀ ਹੱਲ ਕਰਨ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਵੇਰੀਏਬਲਾਂ ਦੇ ਕ੍ਰਮਵਾਰ ਖਾਤਮੇ ਦੀ ਕਲਾਸੀਕਲ ਵਿਧੀ ਹੈ। ਇਸਦਾ ਨਾਮ ਜਰਮਨ ਗਣਿਤ-ਸ਼ਾਸਤਰੀ ਕਾਰਲ ਫ੍ਰੀਡਰਿਕ ਗੌਸ (1777-1885) ਦੇ ਨਾਮ ਉੱਤੇ ਰੱਖਿਆ ਗਿਆ ਹੈ।
ਪਰ ਪਹਿਲਾਂ, ਆਓ ਯਾਦ ਕਰੀਏ ਕਿ SLAU ਇਹ ਕਰ ਸਕਦਾ ਹੈ:
- ਇੱਕ ਹੀ ਹੱਲ ਹੈ;
- ਹੱਲ ਦੀ ਇੱਕ ਅਨੰਤ ਗਿਣਤੀ ਹੈ;
- ਅਸੰਗਤ ਹੋਣਾ, ਭਾਵ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ।
ਵਿਹਾਰਕ ਲਾਭ
ਗੌਸ ਵਿਧੀ ਇੱਕ SLAE ਨੂੰ ਹੱਲ ਕਰਨ ਦਾ ਇੱਕ ਵਧੀਆ ਤਰੀਕਾ ਹੈ ਜਿਸ ਵਿੱਚ ਤਿੰਨ ਤੋਂ ਵੱਧ ਰੇਖਿਕ ਸਮੀਕਰਨਾਂ ਸ਼ਾਮਲ ਹਨ, ਅਤੇ ਨਾਲ ਹੀ ਉਹ ਸਿਸਟਮ ਜੋ ਵਰਗ ਨਹੀਂ ਹਨ।
ਗੌਸ ਵਿਧੀ ਦਾ ਸਿਧਾਂਤ
ਵਿਧੀ ਵਿੱਚ ਹੇਠ ਦਿੱਤੇ ਕਦਮ ਸ਼ਾਮਲ ਹਨ:
- ਸਿੱਧਾ - ਸਮੀਕਰਨਾਂ ਦੀ ਪ੍ਰਣਾਲੀ ਨਾਲ ਸੰਬੰਧਿਤ ਵਧਿਆ ਹੋਇਆ ਮੈਟ੍ਰਿਕਸ, ਕਤਾਰਾਂ ਦੇ ਉੱਪਰਲੇ ਤਿਕੋਣ (ਸਟੈਪਡ) ਰੂਪ ਤੱਕ ਘਟਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ, ਭਾਵ ਮੁੱਖ ਵਿਕਰਣ ਦੇ ਹੇਠਾਂ ਸਿਰਫ ਜ਼ੀਰੋ ਦੇ ਬਰਾਬਰ ਤੱਤ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ।
- ਵਾਪਸ - ਨਤੀਜੇ ਵਾਲੇ ਮੈਟ੍ਰਿਕਸ ਵਿੱਚ, ਮੁੱਖ ਵਿਕਰਣ ਦੇ ਉੱਪਰਲੇ ਤੱਤ ਵੀ ਜ਼ੀਰੋ (ਹੇਠਲੇ ਤਿਕੋਣ ਦ੍ਰਿਸ਼) 'ਤੇ ਸੈੱਟ ਕੀਤੇ ਜਾਂਦੇ ਹਨ।
SLAE ਹੱਲ ਉਦਾਹਰਨ
ਆਉ ਗੌਸ ਵਿਧੀ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਹੇਠਾਂ ਰੇਖਿਕ ਸਮੀਕਰਨਾਂ ਦੀ ਪ੍ਰਣਾਲੀ ਨੂੰ ਹੱਲ ਕਰੀਏ।
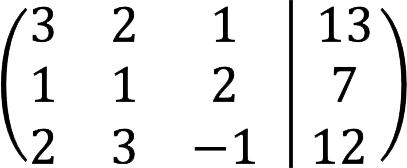
ਦਾ ਹੱਲ
1. ਸ਼ੁਰੂ ਕਰਨ ਲਈ, ਅਸੀਂ SLAE ਨੂੰ ਇੱਕ ਵਿਸਤ੍ਰਿਤ ਮੈਟ੍ਰਿਕਸ ਦੇ ਰੂਪ ਵਿੱਚ ਪੇਸ਼ ਕਰਦੇ ਹਾਂ।
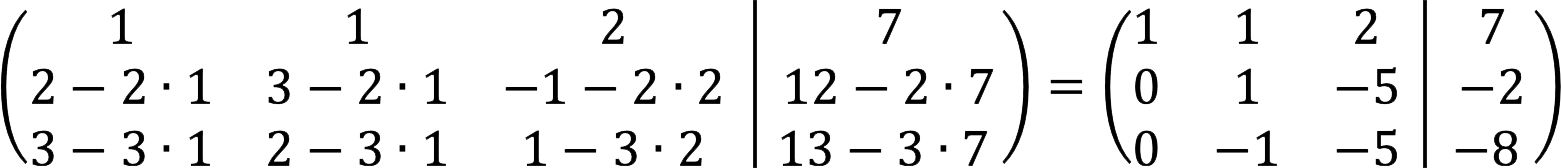
2. ਹੁਣ ਸਾਡਾ ਕੰਮ ਮੁੱਖ ਵਿਕਰਣ ਦੇ ਹੇਠਾਂ ਸਾਰੇ ਤੱਤਾਂ ਨੂੰ ਰੀਸੈਟ ਕਰਨਾ ਹੈ। ਹੋਰ ਕਾਰਵਾਈਆਂ ਖਾਸ ਮੈਟਰਿਕਸ 'ਤੇ ਨਿਰਭਰ ਕਰਦੀਆਂ ਹਨ, ਹੇਠਾਂ ਅਸੀਂ ਉਹਨਾਂ ਦਾ ਵਰਣਨ ਕਰਾਂਗੇ ਜੋ ਸਾਡੇ ਕੇਸ 'ਤੇ ਲਾਗੂ ਹੁੰਦੀਆਂ ਹਨ। ਪਹਿਲਾਂ, ਅਸੀਂ ਕਤਾਰਾਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਕਰਦੇ ਹਾਂ, ਇਸ ਤਰ੍ਹਾਂ ਉਹਨਾਂ ਦੇ ਪਹਿਲੇ ਤੱਤਾਂ ਨੂੰ ਚੜ੍ਹਦੇ ਕ੍ਰਮ ਵਿੱਚ ਰੱਖਦੇ ਹਾਂ।
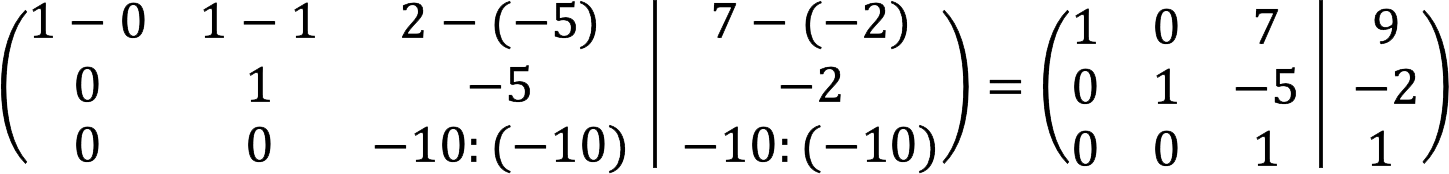
3. ਦੂਜੀ ਕਤਾਰ ਤੋਂ ਪਹਿਲੀ ਤੋਂ ਦੋ ਵਾਰ ਘਟਾਓ, ਅਤੇ ਤੀਜੀ ਤੋਂ - ਪਹਿਲੀ ਤੋਂ ਤਿੰਨ ਗੁਣਾ ਕਰੋ।
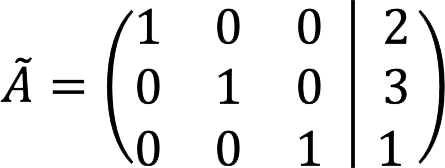
4. ਦੂਜੀ ਲਾਈਨ ਨੂੰ ਤੀਜੀ ਲਾਈਨ ਵਿੱਚ ਜੋੜੋ।
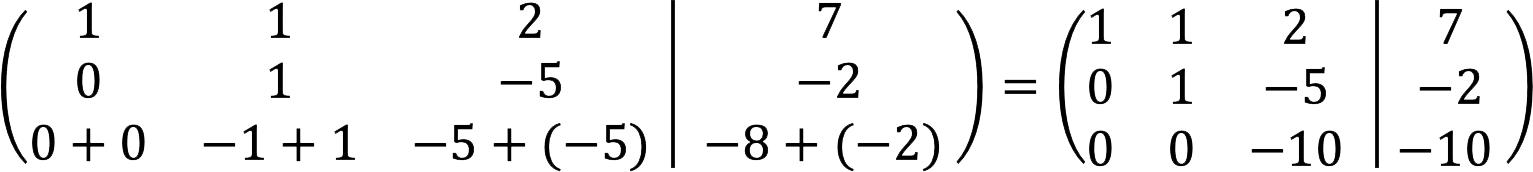
5. ਪਹਿਲੀ ਲਾਈਨ ਤੋਂ ਦੂਜੀ ਲਾਈਨ ਨੂੰ ਘਟਾਓ, ਅਤੇ ਉਸੇ ਸਮੇਂ ਤੀਜੀ ਲਾਈਨ ਨੂੰ -10 ਨਾਲ ਵੰਡੋ।
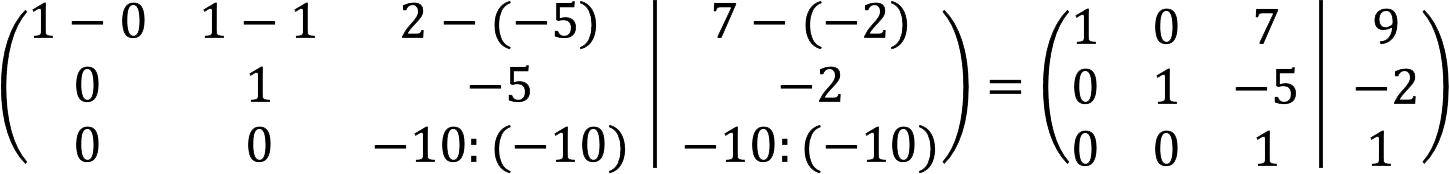
6. ਪਹਿਲਾ ਪੜਾਅ ਪੂਰਾ ਹੋ ਗਿਆ ਹੈ। ਹੁਣ ਸਾਨੂੰ ਮੁੱਖ ਵਿਕਰਣ ਦੇ ਉੱਪਰ null ਐਲੀਮੈਂਟਸ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਲੋੜ ਹੈ। ਅਜਿਹਾ ਕਰਨ ਲਈ, ਪਹਿਲੀ ਕਤਾਰ ਤੋਂ ਤੀਜੇ ਗੁਣਾ 7 ਨੂੰ ਘਟਾਓ, ਅਤੇ 5 ਨਾਲ ਤੀਜੇ ਗੁਣਾ ਨੂੰ ਦੂਜੀ ਵਿੱਚ ਜੋੜੋ।
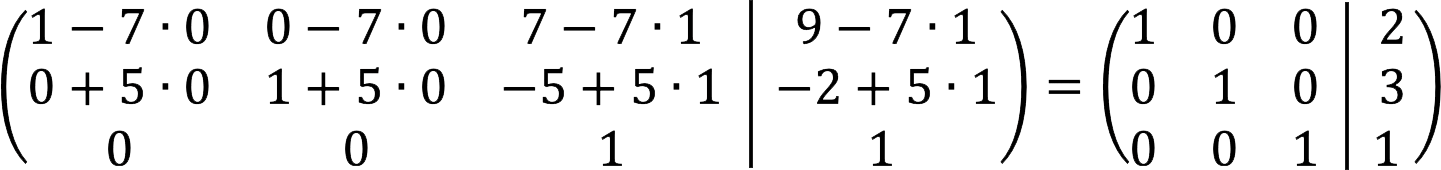
7. ਅੰਤਮ ਵਿਸਤ੍ਰਿਤ ਮੈਟ੍ਰਿਕਸ ਇਸ ਤਰ੍ਹਾਂ ਦਿਖਦਾ ਹੈ:
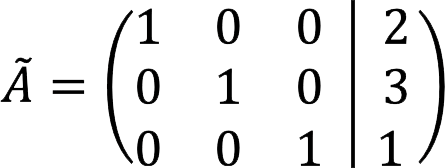
8. ਇਹ ਸਮੀਕਰਨਾਂ ਦੀ ਪ੍ਰਣਾਲੀ ਨਾਲ ਮੇਲ ਖਾਂਦਾ ਹੈ:
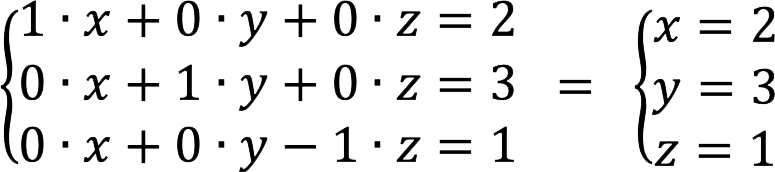
ਉੱਤਰ: ਮੂਲ SLAU: x = 2, y = 3, z = 1.










